What Is Heisenberg’s uncertainty
- Arjun
- Nov 14, 2023
- 3 min read
The uncertainty principle is one of the most important but at the same time also the most misinterpreted equations of quanta’s mechanics. It is an idea that is so absurd and perplexing that has caused great scientists such as Einstein to refute it. However, over the last century, this theory has been tested to be true. It states that there is an innate state of “fuzziness” in the fabric of the universe, a fundamental uncertainty about what we can know. Rather, only a probability about the physical properties exists. This may seem very counter intuitive (in fact, it really is!). In our regular Newtonian life calculating the speed and position is very simple and straightforward. We can know that the speed of a car is 40km/hr and where exactly itt is located. However in quantum mechanics making such calculations about a particle is not possible.
“The uncertainty principle states that we cannot know both the position and speed of a particle, such as a photon or electron, with perfect accuracy; the more we nail down the particle's position, the less we know about its speed and vice versa.” (Science exchange caltech)
This means that if you were to shrink to a size of an electron, we could only calculate your precise position OR speed but not both. This is possible because the particle exists as a wave and particle. How can this be? To know this, we must first understand what does it mean to be a particle and what does it mean to be a wave. Particles by definition can only exist at a particular place at any time. Waves on the other hand are disturbances spread out in space like ripples on water. They have no specific location but do have properties as a whole. The property I would like to focus at is wavelength which is the distance between the two highest or lowest points of a wave. This is essential for quantum mechanics as it represents momentum(mass x velocity). A 1000kg car moving at 30 km/hr has a lot of momentum due to its high mass and a bullet also has a lot of momentum due to its high velocity. A body with a lot of momentum will have a very small wavelength and vice versa. This means that the heisenberg’s uncertainty principle is always there! However, it just has too small of a wavelength for it to ever have an impact on our lives. As even a 100g ball travelling at 10 m/s will have a wavelength of 6.626 x 10^-14. Particles like electrons have a very small mass (9.1093837 × 10^-31 kilograms) so have a wavelength big enough for us to notice in labs.
Thus we can measure the wavelength and thereby measure its momentum, but it has no fixed position. Particles, however, do have a fixed position but no wavelength. Therefore to know the momentum and position of a particle we need a wave which is localised in space meaning it has a small area. We can do this by combining different wavelengths together. This is because when we add waves, where the peaks line up, it forms an even bigger wave as shown in the image.
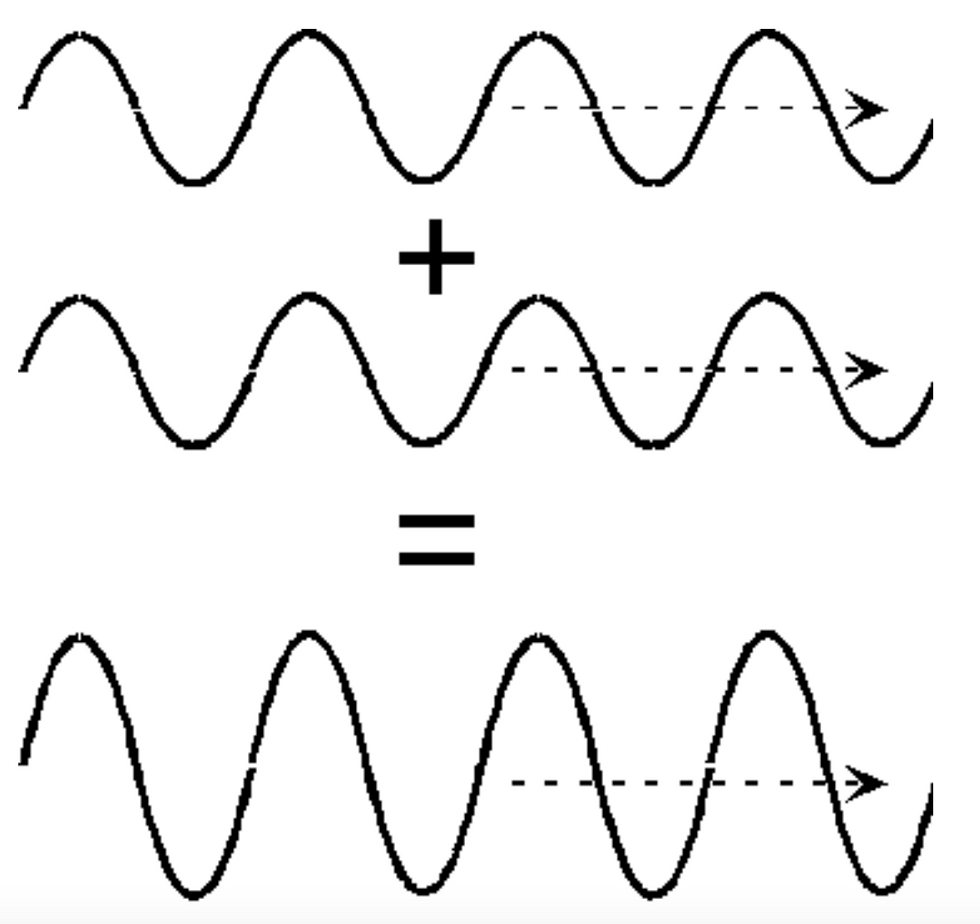
And where the peaks and valleys add up,they cancel each other as shown in the image below.
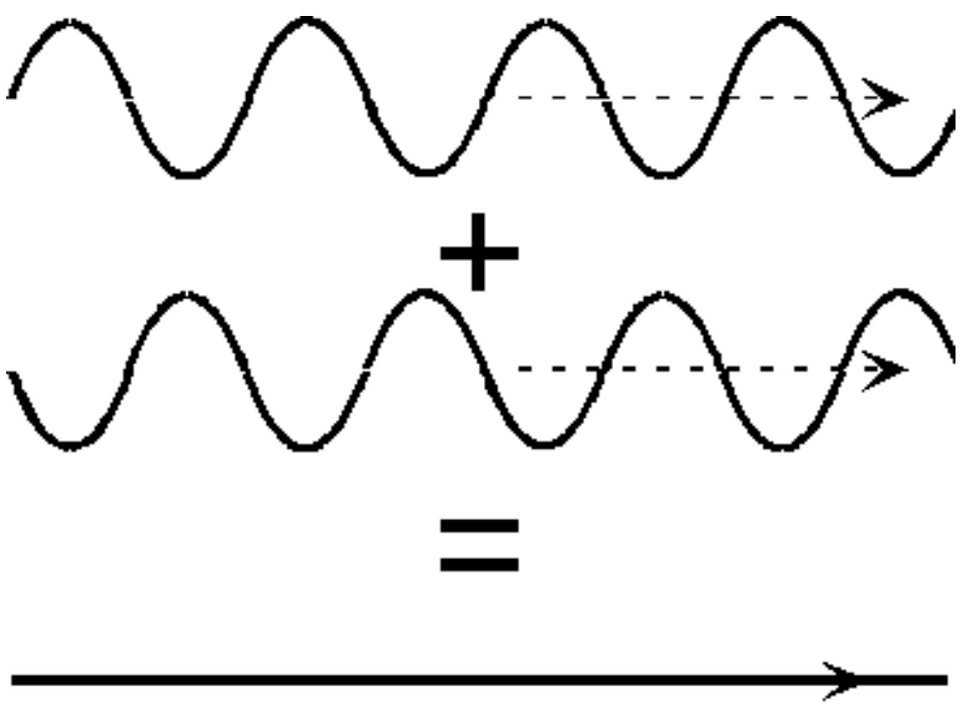
When we keep on adding waves, the regions where the waves cancel out become bigger. This causes the wavelength to become smaller and smaller causing the momentum to become more defined. If we keep adding the waves, we create a wave packet with one precise wavelength at one place. We have thus made a wave packet. This has a position which is in between the wavelength and the the momentum is also uncertain as we used various wavelengths to get the 1 wavelength wave packet. Therefore, more we want to know about the position more the wavelengths we will need to add making the momentum more uncertain and vice versa.
Bibliography




Comments